The Weibull model of the multipath fading channel - Open Research Data - Bridge of Knowledge

Your account

login

Search

The Weibull model of the multipath fading channel

Description

The dataset contains the results of simulations that are part of the research on modelling the multipath fading in the communication channel. The Weibull fading envelope is generated using the Monte-Carlo simulation (MCS) in the LabVIEW programming environment.

The term small-scale fading denotes the rapid variations of the envelope of a received signal. The statistics of the received signal in a mobile radio environment are obtained by using the scattering model and the assumption of large number of randomly phased components. Then the probability density function of the signal envelope has a Rayleigh distribution. Another distribution used to fading model in a multipath environment is the Weibull distribution. This distribution seems to exhibit good fit to the experimental fading channel measurements, for indoor and outdoor environments. The probability density function of the envelope is given by Equation (1). In the special case when a shape parameter is equal to 2, the equation (1) describes the Rayleigh distribution. The parameter of the Weibull distribution r0 is explain by equation (2). The mean value and variance for Weibull fading envelope are given by Equations (3) and (4), respectively. The Weibull envelope can be also written down as a function of the in-phase and quadrature components that specifying the model applied in MCS (Equations 5).

The MCS provides a general approach to numerically approximating the distribution function for the value of the output quantity R(t) = f(X) (where R(t) is a single (scalar) output quantity. X represents the N input quantities (X1(t), . . . ,XN(t))T .

The inputs to the Monte Carlo simulation procedure are:

- the model R(t) = f(X),

- the probability density functions for input quantities X1(t), . . . ,XN (t),

- the number M of Monte Carlo trials.

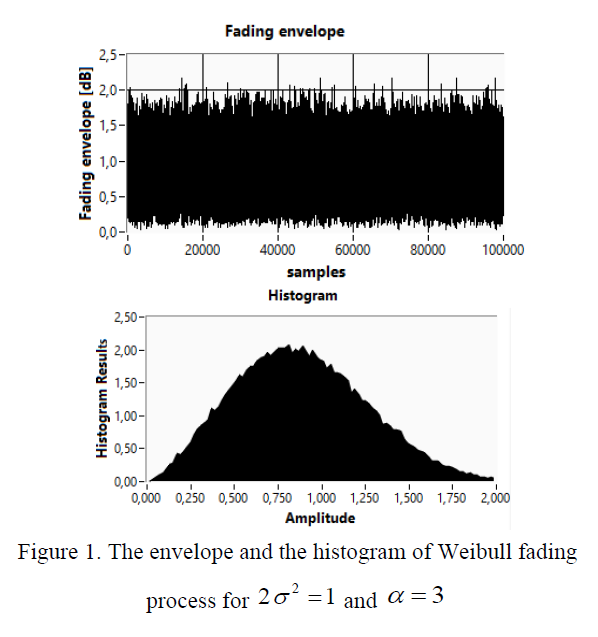
The probability density functions for X=X1(t) Y=X2(t) are a Gaussian type. The number of Monte Carlo trials is equal to 100 000. The exemplary simulation results are shown in Fig. 1.

The simulations were carried out for the Weibull variance equal to 0.5 (Equation 6), and different values of the shape parameter of the Weibull distribution.

The attached files contain two columns related to fading envelope: the number of samples and the amplitude of fading envelope in [dB] and two columns related to the histogram: the number of bins and the histogram results in percents of total amplitude. Files can be opened in both the LabVIEW software and Windows Office Notepad.

The files are described as follows: MCS_Weibull_value of the shape parameter.

 

Illustration of the publication
Illustration of the publication

Dataset file

MCS_Weibull.zip
6.4 MB, S3 ETag 7074ad7432fcb1e938f3935844af0758-1, downloads: 112
The file hash is calculated from the formula
hexmd5(md5(part1)+md5(part2)+...)-{parts_count} where a single part of the file is 512 MB in size.

Example script for calculation:
https://github.com/antespi/s3md5
download file MCS_Weibull.zip

File details

License:
Creative Commons: by-nc 4.0 open in new tab
CC BY-NC
Non-commercial

Details

Year of publication:
2021
Verification date:
2021-05-31
Dataset language:
English
Fields of science:
  • information and communication technology (Engineering and Technology)
DOI:
DOI ID 10.34808/98n4-k804 open in new tab
Series:
Verified by:
Gdańsk University of Technology

Keywords

References

Cite as

Authors

seen 501 times